[DM-02-027] Relationships between Geographic Phenomena
The purpose of geographic information systems is to represent and analyze geographic phenomena, including entities. An important part of any entity is the set of relationships it has with other entities; such relations are crucial to the nature of geography and geographic inquiry. Relationships are commonly stored in spatial databases in a number of ways, and a variety of tools are available to analyze them.
Tags
Author & citation
Plewe, B. (2025). Relationships between Geographic Phenomena. The Geographic Information Science & Technology Body of Knowledge (Issue 2, 2025 Edition), John P. Wilson (ed.). DOI: 10.22224/gistbok/2025.2.3.
Explanation
- Prerequisite Definitions
- Introduction
- Formalizing Relationships
- Relationships in Geospatial Data
- Relationships in Spatial Analysis
- Conclusions
1. Prerequisite Definitions
- Data Model: a design for structuring information in a computer database, at any of several degrees of specificity: a conceptual model represents how information makes sense to people, a logical model is a general strategy for digital representation, and a physical model is the documentation of exactly how data will be structured in the computer. See Relational DMBS and their Spatial Extensions, Logical Data Models, and Physical Data Models.
- Distance Decay: 1) the concept that the strength of a relationship between two entities tends to wane with increasing distance between them. 2) a mathematical model of this tendency. See Proximity and Distance Decay.
- Entity (frequently synonymous with object or feature): A discrete geographic phenomenon with its own existence, identity, properties, lifespan, and spatial extent. See Entity-based Models.
- Field (roughly synonymous with statistical surface, spatially intensive variable, or localized variable). An attribute or property (qualitative or quantitative) that varies over continuous space, such as temperature or density. See Field-Based Representation of Space and Time.
- Network: 1) a collection of connected entities (usually linear) through which something moves or flows. 2) A dataset that models the above. See Networks.
- Ontology: 1) the philosophical study of the nature of being, that is the nature of things that exist in the real world. 2) A structured, documented conceptual model of a particular domain, focused on a controlled terminology of the relevant phenomena and the semantics of the terms of discourse. See Philosophical Perspectives and Foundational Ontologies.
- Relational database: a collection of information structured according to a theory developed in the early 1970s, which collects information into relations (more commonly known as tables), with the ability to connect tables together using joins. See Relational Database Management Systems (DBMSs) and their Spatial Extensions.
- Relationship: A connection between two or more phenomena, of any form or type.
- Spatial Autocorrelation: A mathematical model of the degree to which nearby locations in a field tend to have similar values. See Spatial Autocorrelation.
2. Introduction
Relationships are a crucial part of any ontology or conceptual model of geographic entities, because they are a crucial part of real-world geographic phenomena and of geographic inquiry. Part of what makes location (and thus geography) important is that things in the world are connected to each other in various ways. In fact, it has long been argued that spatial relationships are even more fundamental to understanding geography than the absolute metric space that forms the basis of GIS (Hartshorne 1949, 120; O’Sullivan 2024, 24). Spatial cognition and spatial language are replete with relations (Kitchen and Blades 2002); if someone asks you where you live, you will not give a measured coordinate, but will describe your home as it relates to other places: “it is in country A, in city B, which is near city C; south of landmark D, along street E.”
The importance of relationships has long been enshrined as half of the core geographic concept of site and situation, in which situation is the set of characteristics of a place in relation to other geographic entities (Murphey 1966, 12; Bednarz et al 2024, 9). In fact, many core concepts of geography and spatial thinking are founded on relationships, such as distance, interaction, networks, hierarchies, proximity, connectivity, movement, and diffusion (NCGE 2012). These concepts form the basis for many of the tools and techniques of spatial analysis (O’Sullivan and Unwin 2003, 35-49).
As a random example, perhaps we want to describe Tarrant County, Texas. Among its potentially useful characteristics would be several connections to other geographic entities (i.e., its situation):
- It is a part of the state of Texas.
- It is in the United States of America.
- It mostly overlaps the city of Fort Worth, but neither is completely within the other; however, it is completely separate from the city of Dallas.
- Fort Worth is its county seat.
- It is adjacent to Dallas County and six other counties.
- Its center is 30 miles due west from the center of Dallas County in a straight line, but 32 miles and an average of 45 minutes via roads.
- It is almost identical to Dallas County (and many other counties in Texas) in area and shape, but it is about 20% smaller in population.
- Both it and Dallas County are counties, which is a kind of government entity.
- Every day, tens of thousands of personal and commercial vehicles travel both ways between Tarrant and Dallas counties; in fact, six freeways cross their common boundary.
- It is part of the DFW Metroplex metropolitan area.
- It contains Texas Christian University and the headquarters of American Airlines.
- It was created by the State of Texas 4 years after the latter became a U.S. State.
- It was created from a portion of Navarro County.
- Through Dallas-Fort Worth International Airport (DFW), which it partially contains, over 250 cities can be directly reached in a few hours.
- Part of the eastern boundary of Fort Worth is defined as the county boundary.
- Fort Worth is formally a sister city of Budapest, Hungary and Mbabane, Eswatini.
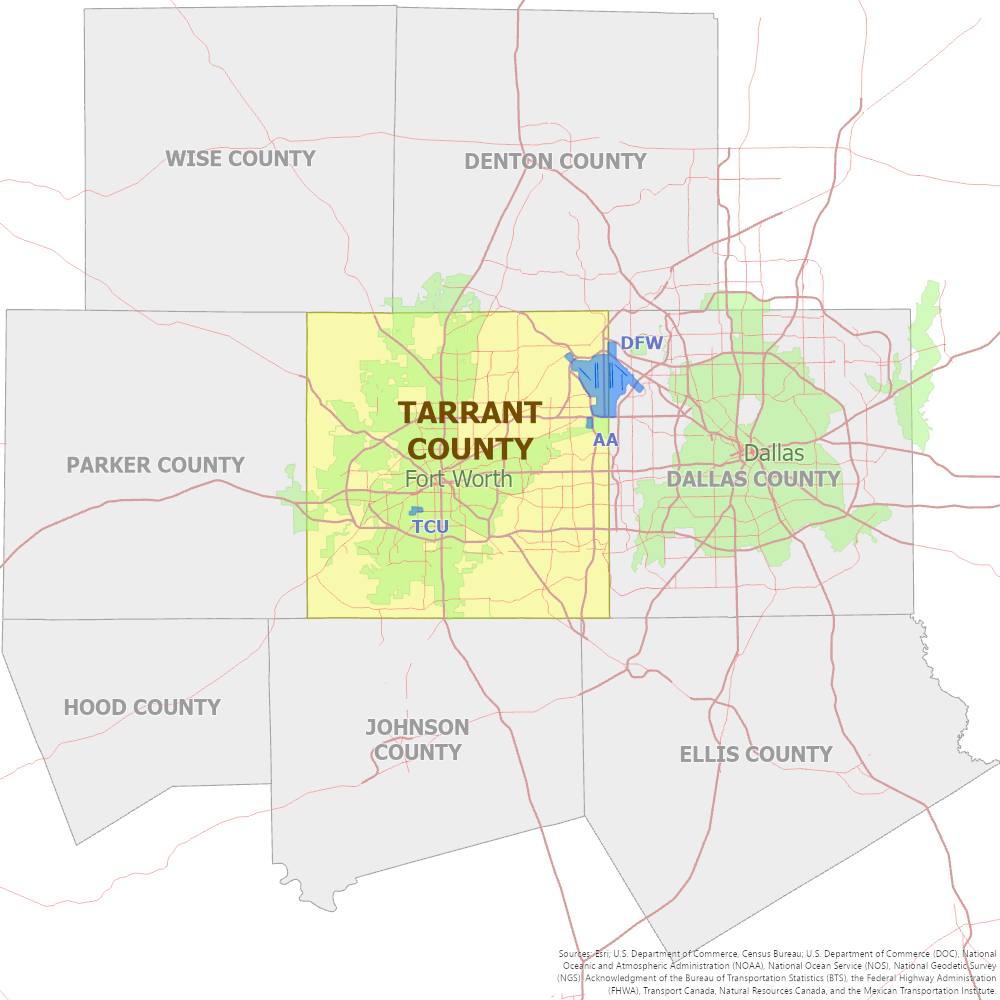
These relationships are quite different from each other, and would be used in different ways in geography and geospatial techniques and technologies. We can group the wide variety of relationships into several categories:
- Topological (#2, 3, 5, 11 above): a qualitative (not measured) spatial relationship, encapsulating whether and how two entities include any shared space. This type of relationship has surely garnered more attention in GIScience scholarship than the others, largely descended from the 9-intersection model, a formal set of possible topological relationships between two-dimensional regions developed by Max Egenhofer, Eliseo Clementini and their colleagues (Egenhofer 1989, Clementini et al 1993). Topological relationships are covered more completely in the Body of Knowledge in topics DM-01-028 and FC-05-018.
- Metric (#6 above): measurable spatial relationships, especially distance and direction. Distance influences many other types of relationships, largely due to the friction of distance, the fact that movement or any other interaction over distance entails a cost (e.g., time, energy) that agents may try to optimize; for example, neighboring cities will likely trade with each other more than distant cities (Hanks 2011, 134). Distance and direction are covered more completely in the GIS&T Body of Knowledge in topics Directional Operations, Proximity & Distance Decay, and Distance Operations.
- Taxonomic (#8): Relationships (usually in a hierarchy structure) between categories (also known as classes, types, kinds, or universals) of phenomena. These are fundamentally different from the other types, because they are between categories of phenomena, while the rest are between individual phenomena. That said, similarity relationships are often used to establish and recognize taxonomic hierarchies, and the fact that two entities belong to the same category (i.e., taxonomic instantiation, 1st half of #8) might be considered a type of similarity relationship.
- Genealogical (#13): Relationships over time between preceding entities and subsequent entities they produce, metaphorically similar to parents and children. Hornsby and Egenhofer (2000), in evaluating the ways in which identity and existence change over time, set forth the basic principles of these relationships between geographic entities (although they did not call them genealogical).
- Meronomic (#1, 10, sometimes called partonomic or aggregation): Relationships between parts and composite wholes, especially when the relationship is crucial to the existence of one or both. Meronomies of events in time are also possible, such as “The Battle of the Bulge was part of World War II.” (Peuquet 1999, 98)
- Definitional (#15): A relationship in which one entity is used to define the location of another entity. A common example is a boundary feature, such as the Oder River forming the boundary between Germany and Poland.
- Functional (#9, #14): Relationships that involve some kind of activity or integration between two entities, such as a volume of trade in goods between two countries. As an example, the Central Place Theory of Walter Christaller, and the many theories of settlement and economic hierarchies it engendered, are attempts to systematize functional relationships (Martin 2005, 509). Distance decay and gravity models are other tools for studying spatial patterns in functional relationships.
- Causal or procedural (first half of #12): A relationship between two phenomena (often events) in the temporal dimension, such that one caused or led to another or that they hold connected, sequential roles in a process.
- Fiat (#4, 16, sometimes called an association): A relationship that exists for no reason other than that it has been formally established by some action. An example would be a treaty between two countries; similarly, related to #14 above, the DFW airport is jointly owned by the cities of Dallas and Fort Worth under a legal agreement between them.
- Similarity (#7): A relationship that is due to two entities being similar in one or more characteristics or attributes. Although distant entities can often be similar by coincidence, it is very common for nearby things to have a strong similarity (frequently due to functional relationships between them), as embodied in Tobler’s First Law of Geography, that “everything is related to everything else, but near things are more related than distant things” (Tobler 1970, 236). This tendency is very common in continuous fields, where it forms the basis of the mathematics of geostatistics, especially spatial autocorrelation (Fotheringham et al 2003, 103; O’Sullivan and Unwin 2003, 180; Griffith 2017).
- Temporal (second half of #12): a relationship in the time dimension between entities or events, which can be qualitative (“The Prussian Kingdom and the French Revolution existed at the same time”) or a quantitative measure (“World War II started 21 years after the end of World War I”). Donna Peuquet and her proteges did much of the pioneering work in understanding the different types of temporal relationships between geographic phenomena, and how to represent them (Peuquet 1999, 97)
Some of these relationship types have received extensive research in geography and geographic information science (especially topology), while others are barely recognized and do not even have a standard term (e.g., definitional, fiat). However, all of them are very common in geographic discourse and geospatial data. Because spatial topological and metric relationships, and the modeling thereof, are well covered elsewhere in the GIS&T Body of Knowledge, this text will focus less on these two types and more on the others.
These types can be organized in several ways. Some are primarily spatial, while others are primarily temporal (see Relationships between Space and Time). Similarity and Functional relationships are not necessarily measured in either dimension, so we might call them adimensional (unless we are studying their spatial patterns, such as with geostatistics).
Some are inherent or identity-based, when the existence of either or both entities are dependent on the relationship (Hornsby and Egenhofer 2000); others are contingent, when there is not such dependence (i.e., they “just happen” to be related). The types can thus be grouped as follows:
Table 1. Relationships among Entities
| Spatial | Temporal | Adimensional | |
|---|---|---|---|
| Contingent-Qualitative | Topological | Time-Topological | Similarity Function |
| Contingent-Quantitative | Metric, Similarity (geostatistics) | Time-Metric | Degree of Similarity, Functional Amount |
| Inherent | Meronomic, Definitional | Genealogical, Causal, Time0-Meronomic | Taxonomic, Instaniation, Fiat |
These various types of relationships are not independent of one another. In fact, much of geographic inquiry involves the search for patterns and causal processes between them. For example, how does the distance between two places influence the amount of functional interaction (e.g., trade, migration) between them (Hanks 2011, 319)? Does that level of interaction influence the degree of similarity (e.g., having a shared language or religion), or could the causal arrow point the other way?
3. Formalizing Relationships
Given the ubiquity of relationships, it should not be surprising that they have been studied in many fields beyond geography and geographic information science. In mathematics, the disciplines of set theory, graph theory, topology, algebra, and formal logic all have significant models of relationships that can be applied to geographic situations.
The philosophical discipline of ontology, the attempt to understand the nature of real-world phenomena, has studied relationships at length, especially mereology, the study of part-whole relationships (Simons 1987, Herre 2010). In computing, ontological philosophies are encoded as formal ontologies and data models, both documentations of how phenomena should be represented in a system (or in general), of which relationships form a crucial part (see Foundational Ontologies). For example, the SUMO general formal ontology (one of several attempts to formally classify all phenomena, not just geography) recognizes several types of “relations,” including meronomic, topological, causal, metric, and temporal.
Ontologies that focus on geographic phenomena have also recognized the importance of relationships. For example, the spatio-temporal ontology of Bittner et al (2006) focuses on meronomy and taxonomy, but acknowledges the existence of topological, temporal, and metric relationships. Tambassi (2016) discusses topology and mereology as requisite components of any geo-ontology.
One useful formal theory that comes from mathematics (primarily set theory) classifies relationship types according to basic logical deductions that can be made from them. This includes three types (Worboys & Duckham 2004, 95):
- A reflexive relation is one in which an entity can be related to itself. For example, the topological relationship coincides (i.e., two entities occupy identical space) is reflexive: a county coincides with itself. Most relationships are not reflexive: a phenomenon cannot occur after itself, or be 45km from itself, or be adjacent to itself.
- A symmetrical relation is one in which a relationship expressed from one entity to another is the same as the relationship in the other direction. For example if A is 45km from B, then B is 45km from A. An example of an asymmetrical relation would be meronomy (if A is part of B, B cannot be part of A) and direction (if A is north of B, B cannot be north of A). In asymmetrical relations, there is often a corresponding inverse relationship (part of/contains, north of/south of).
- A transitive relation is one in which given that A is related to B and B is related to C, then A is related to C. For example, most topological and meronomic relationships are transitive: Tarrant County is a part of Texas, and Texas is a part of the United States, so Tarrant County is a part of the United States. Many other types of relationships are not transitive, such as genealogy: Iowa Territory was created from Wisconsin Territory and Wisconsin Territory was created from Michigan Territory, but Iowa Territory was not created from Michigan Territory.
Because relationships are an important part of domains that produce data, not just geography, they have also been studied in computer science. An important tool that our discipline has adopted is the use of data modeling tools to design a database, such as Entity-Relationship (E-R) diagrams (Chen 1976) and the Unified Modeling Language (UML) class diagram (OMG 2017). These diagrams visually depict the kinds of things that will be represented in a database, and the real-world relationships between them that will also be stored (see Figure 2).
4. Relationships in Geospatial Data
As with many aspects of ontology, it is easy to see the above theorizing as an esoteric philosophical exercise with little practical value. However, relationships of all of these types are ubiquitous in geospatial data, so their intentional management has practical value.
As a case study, let us look at one of the most prevalent types of GIS database, the cadastre (also known as a parcel fabric). In the United States, such data is almost always maintained by county governments, while other countries maintain land records at the provincial (e.g., Canada, Australia, Germany, Switzerland) or national (e.g., most of Europe) level. This type of GIS data is so ubiquitous because it is the basis for several crucial functions, including the assessment of property taxes, urban planning, land use zoning, recording land transactions, and the guarantee of title (i.e., proving that person A owns the property so they can legally sell it to person B).
To accomplish these purposes, a typical parcel GIS needs to store several relationships:
- The fact that this is a parcel like all the other parcels: taxonomic instantiation
- The city and/or other taxing entities in which it is situated: topological
- The subdivision of which it is a part: meronomic
- The county (in the U.S.) in which it is recorded: meronomic
- The legal document that first created it, such as a subdivision plat: causal
- The “parent” parcel(s) that covered the space immediately before this parcel was created: genealogical
- The current owner: fiat
- The measured lines (legally defined distances and directions) and survey monuments that form its boundary, often stored in separate data layers: definitional
- The street along which it is addressed: topological
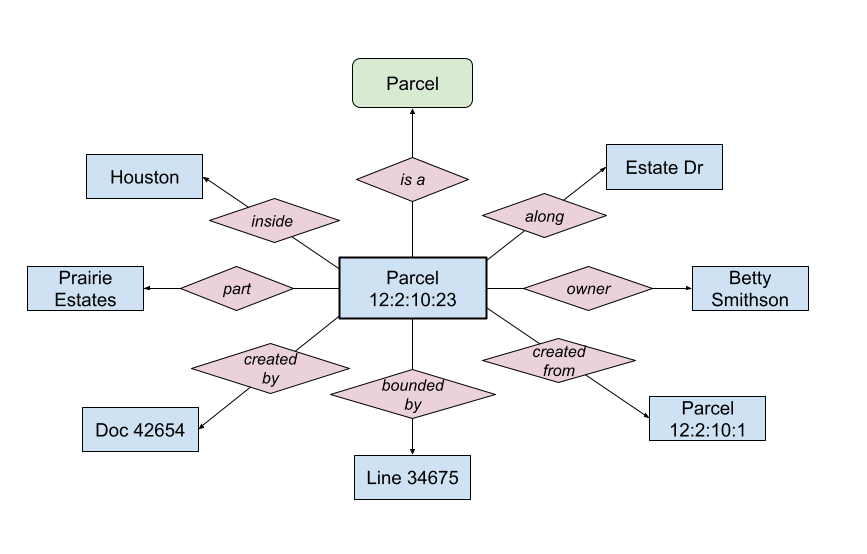
These relationships may be stored in a number of ways in a spatial database, which is usually based on a relational database model (see Relational Database Management Systems (DBMSs) and their Spatial Extensions).
- All of the parcel instances are likely stored in a single structure, such as a file, table, feature class, or layer; in fact, this collecting of taxonomically related objects is the origin of the term relation in the relational database model.
- Store a relation as a simple text or numeric attribute, typically the name or identifier of the related entity (e.g., land use code, city name).
- Store a foreign key in the attributes that points to the related feature in the same table (e.g. parent parcel) or another table (subdivisions, recorded documents).
- In a relational database, a many-to-many relationship (e.g. parcels to boundary lines) is usually recorded using a third linking table. This linking table is essentially a model of the relationship itself, and has the advantage of being able to store not only the existence of a relationship, but also any properties of that relationship (e.g., when it began or ended, source citations).
In addition to the relational databases that have traditionally been the basis of GIS, other architectures have become increasingly popular in recent years (see NoSQL Databases). One example, the graph database is especially relevant because it is fundamentally organized around the storage of relationships as edges between nodes, the entities (O’Sullivan 2024, 41). Another similar architecture, the semantic web based on the Resource Description Framework (RDF) data model, also uses a model that lends itself to the explicit representation of relationships. RDF stores data as a set of subject-predicate-object statements or triples; for a relationship, the subject and object are both entities, such as “parcel:12-2-10-23 rel:created_from parcel:12-2-10-1.”
Topological relationships are not usually explicitly stored in GIS databases when they are purely contingent. However, some kinds of inherent relationships can manifest as topology, especially definitional (boundary line features should line up with the edges of polygons) and meronomic (parts should be within their wholes), and it is often useful to represent these in geospatial data. GIS&&T Body of Knowledge topics The Topological Model (forthcoming) and Spatial Network Modeling address the various techniques for modeling topological data.
5. Relationships in Spatial Analysis
While explicit storage in a database is the common solution for representing inherent relationships, it is not as common for contingent relationships, largely for the simple reason that they may not be known a priori. Instead, they are usually discovered using the tools of spatial analysis. One of the oldest tools for doing this is polygon overlay (first introduced in the late 1960s), which uses two or more polygon datasets to create a new one based on the topological relationships between their features (see Overlay). In a similar fashion, spatial query searches for features based on their topological relationships to other features (see Spatial Queries), and spatial join merges the attribute tables of two layers based on their topological relationships. Some current GIS software also allows for spatial joins based on contingent metric relationships (i.e., distance).
Perhaps no branch of GIS analysis encapsulates more of the scope of spatial relationships than network analysis, commonly used for managing networks ranging from telecommunications to utilities to transportation (O’Sullivan 2024, 145). Network datasets require information about topology to know how elements are connected to each other. The analysis of movement and flow through the network is typically based on the functional and metric relationships between places (nodes) in the network, such as finding the shortest route from point A to point B.
The acknowledgment of spatial relationships (especially spatial autocorrelation) is what differentiates spatial statistics and geostatistics from other forms of statistical analysis. The fact that an observed value at a sample location in space is rarely independent of its surroundings (including nearby sample data) breaks one of the fundamental assumptions of most statistical methods; spatially aware methods such as kriging and geographically weighted regression take advantage of spatial similarity and other relationships to produce more accurate results (Fotheringham et al 2002; Wu and Kemp, 2019; Hoffman and Kedron, 2023; Sachdeva and Fotheringham, 2020).
During the Quantitative Revolution of the 1950s and 1960s, geographers adopted several mathematical models of relationships from physics, such as the inverse square law that models the strength of everything from light to gravity based on distance. In geography, it has been found that many kinds of quantitative relationships between two entities, especially similarity and functional integration, are strongly negatively correlated with the the distance between them, a concept commonly called distance decay (see Proximity and Distance Decay). That is, if one person lives further from a store than another person, they are less likely to shop there, assuming all other factors such as brand preference are the same. Unlike physical relationships such as gravity and magnetism, most geographic relationships do not follow this pattern exactly, but enough for it to be a useful basis for modeling. These kinds of relationships are generally studied using the techniques of spatial interaction modeling (see Spatial Interaction).
6. Conclusions
At first glance, relationships may not seem central to the world of GIS, with its basis in absolute coordinate locations and its focus on how to represent and analyze distinct entities and property fields. Frankly, there is not an extensive GIScience literature studying them as a distinct subject matter; rather, they are often taken for granted as a mundane aspect of geographic phenomena and geospatial data.
However mundane, they are ubiquitous and crucial to understanding and managing our geography. Any exercise to design GIS databases or analytical procedures is well served by being intentional about how to model relationships.
References
- Bednarz, S. W., Bockenhauer, M. H., and Hiebert, F. T. (2024). Human Geography: A Spatial Perspective. Boston: Cengage
- Bittner, T., Donnelly, M., & Smith, B. (2009). A spatio-temporal ontology for geographic information integration. International Journal of Geographical Information Science, 23(6), 765–798.
- Chen, P. (1976). The Entity–Relationship Model – Toward a Unified View of Data. ACM Transactions on Database Systems. New York: Association for Computing Machinery. 1(1): 9–36.
- Clementini, E., Di Felice, P., van Oosterom, P. (1993). A small set of formal topological relationships suitable for end-user interaction. In: Abel, D., Chin Ooi, B. (eds) Advances in Spatial Databases. SSD 1993. Lecture Notes in Computer Science, vol 692. Springer, Berlin, Heidelberg
- Duckham, M., and Worboys, M. (2004). GIS – A Computing Perspective. 2nd Edition. CRC Press.
- Egenhofer, M.J. (1989). A formal definition of binary topological relationships. In: Litwin, W., Schek, HJ. (eds) Foundations of Data Organization and Algorithms. FODO 1989. Lecture Notes in Computer Science, vol 367. Springer, Berlin, Heidelberg.
- Fotheringham, A. S., Brunsdon, C., & Charlton, M. (2003). Geographically Weighted Regression: The Analysis of Spatially Varying Relationships. John Wiley & Sons.
- Griffith, D. (2017). Spatial Autocorrelation. The Geographic Information Science & Technology Body of Knowledge (4th Quarter 2017 Edition), John P. Wilson (ed).
- Hanks, R. R. (2011). Encyclopedia of Geography Terms, Themes, and Concepts. Santa Barbara, CA: ABC-CLIO.
- Hartshorne, R. (1949). The Nature of Geography: A Critical Survey of Current Thought in the Light of the Past, 2nd Edition. Association of American Geographers.
- Herre, H. (2010). The Ontology of Mereological Systems: A Logical Approach. In: Poli, R., Seibt, J. (eds) Theory and Applications of Ontology: Philosophical Perspectives. Springer, Dordrecht.
- Hoffman, T. D. and Kedron, P. (2023). Spatial Autoregressive Models. The Geographic Information Science & Technology Body of Knowledge (2nd Quarter 2023 Edition). John P. Wilson (Ed.).
- Hornsby, K. and Egenhofer, M.J. (2000). Identity-based change: a foundation for spatio-temporal knowledge representation. International Journal of Geographical Information Science 14, 207–224.
- Martin, G. J. (2005). All Possible Worlds: A History of Geographical Ideas, 4th Edition. Oxford University Press.
- Murphey, R. (1966). An Introduction to Geography. Rand McNally.
- National Council for Geographic Education (NCGE). (2012). Geography Standard 3: The World in Spatial Terms, in National Geography Standards, 2nd Edition.
- O'Sullivan, D. and Unwin, D. (2003). Geographic Information Analysis, 1st Edition. Hoboken, NJ: John Wiley & Sons.
- O’Sullivan, D. (2024). Computing Geographically: Bridging GIScience and Geography. New York: Guilford.
- Object Management Group (OMG). (2017). Unified Modeling Language, Version 2.5.1.
- Peuquet, D. (1999). Time in GIS and Geographical Databases, Chapter 8 in Longley, Paul A., Michael F. Goodchild, David J. Maguire, and David W. Rhind (eds.), Geographical Information Systems, Wiley and Sons.
- Sachdeva, M. and Fotheringham, A. S. (2020). The Geographically Weighted Regression Framework. The Geographic Information Science & Technology Body of Knowledge (4th Quarter 2020 Edition), John P. Wilson (ed.).
- Simons, P. (1987). Parts – A Study in Ontology. Oxford: Clarendon Press.
- Tambassi, T. (2016). Rethinking Geo-Ontologies from a Philosophical Point of View, Journal of Research and Didactics in Geography, 2:5 (Dec 2016) pp.51-62.
- Tobler, W. R. (1970). A Computer Movie Simulating Urban Growth in the Detroit Region. Economic Geography 46: 234–240.
- Wu, A.-M., and Kemp, K. K. (2019). Global Measures of Spatial Association. The Geographic Information Science & Technology Body of Knowledge (1st Quarter 2019 Edition), John P. Wilson (Ed.).
Learning outcomes
-
1918 - List the relationship characteristics of a given geographic phenomenon.
List the relationship characteristics of a given geographic phenomenon.
-
1919 - Describe the types of relationships that would be important to model for a given geographic task.
Describe the types of relationships that would be important to model for a given geographic task.
-
1920 - Determine the appropriate data models and architecture(s) for modeling the particular types of relationships needed in a newly designed geospatial database.
Determine the appropriate data models and architecture(s) for modeling the particular types of relationships needed in a newly designed geospatial database.
-
1921 - Design and carry out analytical and modeling procedures that effectively incorporate and evaluate relationships.
Design and carry out analytical and modeling procedures that effectively incorporate and evaluate relationships.
Related topics
- [AM-02-004] Overlay
- [AM-03-010] Spatial Interaction
- [AM-03-022] Global Measures of Spatial Association
- [DM-01-028] Topological Relationships
- [DM-02-013] The topological model
- [DM-02-015] Spatial Network Modeling
- [FC-05-014] Directional Operations
- [FC-05-017] Proximity and Distance Decay
- [FC-05-018] Adjacency and connectivity
- [FC-06-013] Spatial Queries