[FC-06-013] Spatial Queries

Yao, X. (2021). Spatial Queries. The Geographic Information Science & Technology Body of Knowledge (1st Quarter 2021 Edition), John P. Wilson (Ed.). DOI: 10.22224/gistbok/2021.1.10.

It is also available in an earlier edition: 

DiBiase, D., DeMers, M., Johnson, A., Kemp, K., Luck, A. T., Plewe, B., and Wentz, E. (2006). Spatial queries. The Geographic Information Science & Technology Body of Knowledge. Washington, DC: Association of American Geographers. (2nd Quarter 2016, first digital).

1. Definitions
2. Introduction to Spatial Queries
3. Performing Spatial Queries

1. Definitions

Spatial Analysis: In GIS, spatial analysis is a collective term that refers to any process that manipulates or synthesize spatial data to explore spatial patterns or to examine spatial relationships among geographical features. It embraces a broad spectrum of spatial data techniques such as spatial queries, vector and raster GIS data handling operations, and spatial statistics.

Spatial query: A search of features based on their spatial relations with other features. It is a crucial comprising part of spatial analysis in GIS.

Spatial relation: A relationship between spatial features with regard to their spatial locations and spatial arrangements. Three general categories of spatial relations have been identified in the GIS&T literature, including proximity (or distance-based) relations, topological relations (e.g., connectivity, containment, and adjacency), and direction relations.

Feature: A digital representation of a geographic object (e.g., a house, a road segment, a county) or event (e.g., a traffic accident) located in space. A feature in a spatial database is represented with data of its spatial footprint and attribute information.

Feature class: a collection of geographic features of the same kind.

Topological relations: The type of spatial relations unaffected by bi-continuous transformation, such as stretching, shifting, rotating, or bending, of the involved spatial features.

Proximity relations: They are also called distance-based relations and refer to the spatial relations based on distances between features.

Direction relations: A spatial relation based on the angular separation of one feature relative to another feature in a coordinate system. Specifically, when the angular separations are expressed verbally as cardinal directions such as north and south, they are also called cardinal direction relations.

2. Introduction to Spatial Queries

2.1 What is a spatial query?

Spatial queries are a critically important type of spatial analysis. A spatial query selects spatial features based on their spatial relationships to other features and are used to answer spatial questions. For instance, a researcher needs to identify crime sites in a study area, and another person tries to find locations of all traffic accidents along some pre-defined roads. These spatial questions can be translated into respective spatial queries. Here spatial queries can be used as the sole spatial analysis method to answer these spatial questions. In addition, spatial queries can also be a constituent part of multi-step spatial analysis.

For explanation, we first define the critical components in a spatial query. The collection of candidate spatial features to be selected from are termed target features, while the spatial features used as reference locations are called reference features. For example, in the query “find buildings in census tract A,” all buildings in the study area are target features, and Tract A is the reference feature. The third component is the spatial relation(s) between the target and reference features.  

Depending on the reference feature type, a spatial query may involve one or more GIS feature classes. The following are three possible scenarios.

1. The reference feature(s) and target features are of the same type and stored in the same GIS files. In this case, only a single GIS feature class is needed. An example query is “which cities are within 200 miles of Atlanta.” Here the reference feature is the pre-defined or pre-selected city (Atlanta), and the target features are also cities. 
2. The reference feature(s) and target features are of different types. In this situation, two feature classes are involved in the spatial query. The abovementioned query “find buildings in census tract A” is an example of this scenario. The two feature classes are the census tract and the buildings.
3. Reference location is created on the fly. Sometimes, a user may wish to conduct a spatial query interactively to select features by a reference location entered on the fly. The interactive spatial queries are particularly popular in web-based GIS services. In this situation, the spatial query only requires target features to be provided in advance.  For instance, the USGS national map viewer is a web service for viewing and downloading GIS data. The service provides GUI tools for users to define a selection boundary by interactively drawing a polygon, a rectangle, or a circle.    

While the target features and reference features are necessary, a query’s critical component is the spatial relation between the two sets of features. Ultimately, the query results are the subset of target features that satisfy the spatial relation. It is demonstrated by the equation below where SR refers to a spatial relation.

Query results = target features [SR] reference features   

2.2 Spatial Relations and Spatial Queries

Three types of spatial relations have been studied and have received considerable research attention in the GIS&T literature: proximity relations, topological relations, and directional relations.

2.2.1 Proximity relations 

Proximity relations are distance-based and are also referred to as distance relations. A proximity relation can be expressed either quantitatively as metric distances or qualitatively as verbal descriptions such as near or far. A GIS software program typically has powerful built-in capabilities to calculate various types of quantitative distance measures.  In spatial queries, the most commonly used are Euclidean distances and distances in a connected network. Table 1 provides a real-world query example for the corresponding distance measure. QE1 (query example 1) searches for buildings in a proximal area exposed to noise hazards from a state highway. It adopts the Euclidean distance to search for buildings within 1 mile of the highway segment. In QE2, the concern is about the travel distances to healthcare facilities. Qualitative expressions of proximity are often needed in spatial queries in everyday lives. For example, QE3 inquiries about nearby hotels of a conference venue in Chicago. Not many GIS programs currently support spatial queries with qualitative proximity relations, although theoretical discussions and modeling strategies are available in the literature. One approach is to establish fuzzy mapping mechanisms between qualitative and quantitative measures, contingent upon context variables (Yao & Thill 2005; 2006). Also, some online GIS services and open-source tools are available to provide spatial search capability with qualitative distances.

Table 1. Query Examples Based on Proximity Relations

Distance Measure	Query Example (QE) & Illustration
Euclidean distance	QE1. Which buildings are located within 1 mile of state highways in the study area?
Network distance	QE2. Which areas are less than 2 miles by driving from healthcare facilities?
Qualitative distance	QE3. Find hotels near the conference venue.

2.2.2 Topological Relations

Topology is a branch of study in mathematics. It studies the characteristics of spatial relations invariant by bi-continuous transformations such as stretching, shifting, rotating, or bending. Adjacency, connectivity, and containment are typical examples of topological relations. A naïve view of topology sees the relations as geometry on a rubber sheet, as topological relations between two spatial features on a rubber sheet are preserved even when the sheet is stretched, shifted, rotated, or bent.  A large body of research has focused on formalizing and reasoning topological relations, ranging from the point-set theory (Egenhofer and Franzosa 1991), the intersection model (Egenhofer and Franzosa 1991) and its extensions, to the Region Connection Calculus (Randell et al. 1992) and its extensions (e.g., Cohn and Gotts 1996).

Depending on the two involved features' geometric types, different sets of possible topological relations may exist between them.  Table 2 illustrates some common topological relations, cross-tabulated by the geometric type of the reference feature(s) and that of the target feature(s) in a spatial query. It is far from an exhaustive enumeration of topological relations. Many other nuanced variations exist, and different vocabulary may be used to describe identical or similar relations. For instance, Egenhofer (1991) discussed more English terms that express topological relations.

Table 2. A Classification of Some Common Topological Relations Between Two Spatial Features

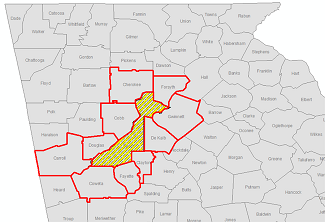
Spatial queries can be based on a variety of topological relations (Table 3). In QE4, a county has multiple internet service providers, and the query is to find which public office locations can be served by a specific provider MP. The polygons in blue are the service areas by MP, which are reference features. The target features are all the point locations of public services and offices. This spatial problem can be translated into the “Contained_by” topological relation between the target features and the reference features. The final query results are shown in red. QE5 can be translated into the “intersect” relation between the reference and target features. QE6 is a query based on the adjacency topological relation.

Table 3. Query Examples Based on Topological Relations

Topological Relation	Query Example (QE) & its Illustration
Contained_by	QE4. Which public office locations are in the service area of the MP Internet service provider?
Intersect	QE5. Which census tracts in Atlanta do the metropolitan subway routes go across?
Adjacent	QE6. What are the neighboring counting of Fulton County?

2.2.3 Direction Relations

Direction relations are based on the angular separation between two spatial objects, as viewed from the reference point. Just like proximity relation, a direction relation can also be expressed either qualitatively or quantitatively. A quantitative measure of the direction from a reference feature to a target feature is relatively easy to calculate in GIS. In Figure 1, the direction-based spatial query is to find buildings in the study area in the downwind from a reference feature (QE7). Different reasoning models may be possible. In this illustrated example, a hypothetical parallelogram is created along the window direction. The query results would include all the buildings that are entirely within or intersect with the parallelogram. 

Figure 1. A direction-based search from a reference feature. Source: author.

Compared with the quantitative directions, qualitative direction measures are used more often. They are also referred to as cardinal directions such as north, south, east, west, southeast, southwest, northeast, and northwest, which are defined by a look-up table indicating the corresponding range of angles for each direction. These cardinal directions are not directly understandable by GISs. Modeling direction relations in a computer system has attracted much research attention in the past decades. The earlier frameworks, such as the cone-shaped (or triangular) model (Peuquet and Zhang 1987) and the projection-based model (Frank 1996), have laid the foundation for more recent extensions. Figure 2(a) illustrates the framework of the cone-based model. Figure 2(b) is an application example of implementing the model for spatial queries. In QE8, the query investigates cabins (target features) to the south of the lake, the reference feature. From the reference feature's geometric center, the model partitions the surrounding geographic space into eight sectors corresponding to the eight cardinal directions, respectively. The target features in the S sector are the query results.

Figure 2. Cone-based model (adapted from Frank 1996) and its application to answer a query example (QE8: “which cabins are to the south of the lake?").  Source: author.

The projection-based model is another influential framework. As shown in Figure 3(a), the projection-based model singles out a central area, which can be the bounding box of the reference feature, and partitions the outside areas into eight regular direction tiles corresponding to the eight cardinal directions. Based on the framework, some spatial analytical models have been further developed to deal with more complex situations or make the process more computationally plausible. Among them, the direction relation matrix (DRM) model is a widely adopted example. The DRM model (Goyal & Egenhofer 2001) formalizes the reasoning process by defining a direction relation with a matrix expressed in Equation (1). If an area is considered a set of all points within that area, the areas in Equation (1) refer to those point sets illustrated in Figure 3(b). The set intersection operation of two sets, denoted as Ç,  produces the subset of points that are in both sets.  The model can deal with more complex situations, for instance, when a target feature crosses multiple direction tiles.

Figure 3. Projection-based model (adapted from Frank 1996).  Source: author. 

Based on the framework, some spatial analytical models have been further developed to deal with more complex situations or make the process more computationally plausible. Among them, the direction relation matrix (DRM) model is a widely adopted example. The DRM model (Goyal & Egenhofer 2001) formalizes the reasoning process by defining a direction relation with a matrix expressed in Figure 4. If an area is considered a set of all points within that area, the areas in the matrix refer to those point sets illustrated in the map of Figure 4. The set intersection operation of two sets, denoted as Ç,  produces the subset of points that are in both sets.  The model can deal with more complex situations, for instance, when a target feature crosses multiple direction tiles.

Figure 4. Illustration of point sets and the definition equation for the direction-relation matrix (adapted from Goyal & Egenhofer, 2001).  Source: author.

2.2.4 Spatial Queries based on Multiple Spatial Relations

A spatial query does not have to be limited to one spatial relation only. It is not rare to find a query based on a combination of multiple spatial relations. This may happen due to several reasons. Discussed here are just two common reasons. First, it may be due to the nature of the query problem. For instance, QE7 and QE8 might need to be modified in the real world to find houses or cabins within certain threshold distances. The modified queries would combine a proximity relation and a direction relation. Second, multiple spatial relations are sometimes necessary with practical considerations of precision or other data quality issues. For example, a user wants to find all traffic accidents on a specific highway. This can be translated into a spatial query based on the topology relation “touch” between a point and a line feature, as listed in Table 2. However, due to precision and accuracy reasons, many qualifying accident locations would be missed if only the “touch” topological relation is considered. The problem can be resolved by modifying the query to include all accident locations within a threshold distance to the line feature. The modified query combines topology and distance relations.  

3. Performing Spatial Queries

As discussed above, spatial reasoning frameworks and analysis models have been developed for each type of spatial relations. Although some of them are integral parts of popular GIS software programs, not all of them have been developed into software tools in the GIS programs. Depending on the availability of functions and tools in off-the-shelf GIS software, there are generally three approaches to carrying out a spatial query. The most popular way is to use inherent spatial query functions in a GIS program. The second is to run SQL statements in GIS or any general-purpose spatial database management system. The last approach is to develop customized tools for queries. While each method has its advantage and disadvantages, the good news is that their edges are complementary to each other.

• Spatial queries with innate functions in GIS software. As the spatial query capability is crucial for GIS, almost all GIS software programs have at least some built-in spatial query functions from the user interface. Currently, all popular GIS programs have innate functions for distance-based queries, except for qualitative distance. Many of them have built-in capabilities to answer spatial queries based on topological relations, and some of them can handle those based on a combination of two spatial relations. Results are returned on-the-fly for interpretation and further processing. This is the most straightforward and most widely used approach. The limitation of this approach lies in the constraints of existing functions provided by the software in use.  
• Spatial queries with structured query language (SQL). Because a spatial query is about selecting features based on spatial relations, it can be expressed as SQL statement(s) by translating the query components into search criteria. The execution of the SQL statement returns spatial features that satisfy the search criteria. This can be conducted in any spatial database management system that supports SQL. Some GIS software provides the interface for SQL expressions. For instance, ArcGIS provides query building dialog tools that allow users to build SQL statements. Likewise, these statements can also be constructed and executed in other database management systems, such as PostgreSQL and Oracle.  Performing a query using SQL statements allows for more flexibility. Compared with the approach using built-in GIS functions, the SQL statements method leaves room for user-designed search criteria, working in a broader selection of software environments. However, writing native SQL queries lacks the interactivity and convenience provided by the built-in functions.   
• Spatial queries with customized tools.  The first two approaches are sufficient for the need of most spatial queries. But in some rare cases, when a unique model is needed or a particular type of query is asked, neither of the previous two approaches may be helpful. The third approach, developing customized software tools, is the solution in this situation. The tools can be loaded as add-in functions to existing GIS software or as stand-alone packages. Some developed tools for specific types of queries have been shared in open-source repositories such as GitHub for interested people to use. This approach is most effort-intensive and requires programming skills. Thus it is the most challenging approach if one has to start from scratch. The tradeoff is that this approach does provide the best flexibility and therefore is most suitable when a high level of customization is needed.